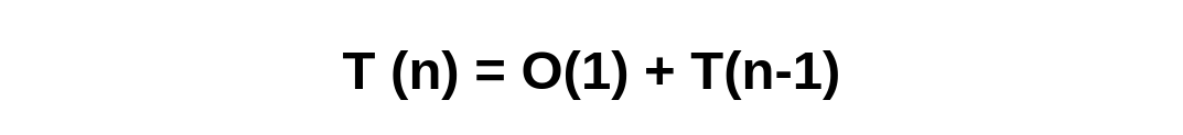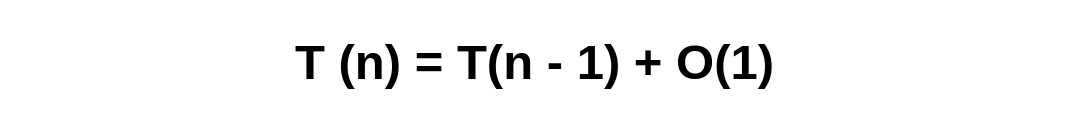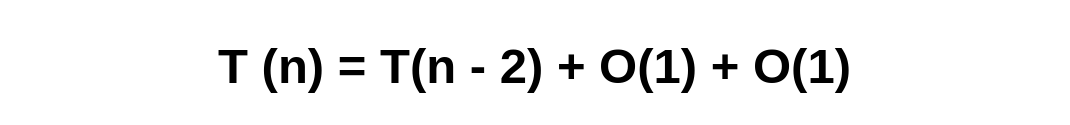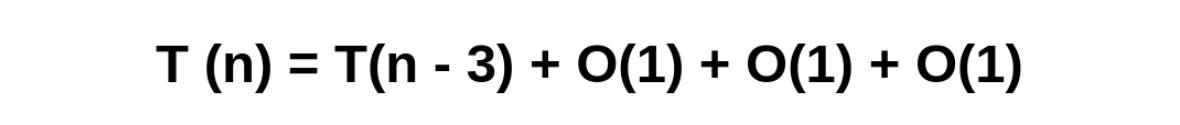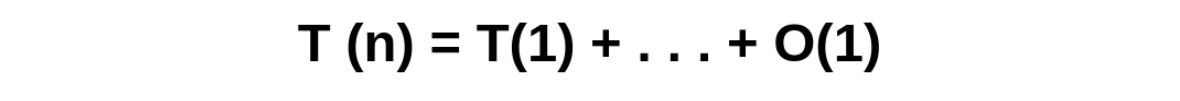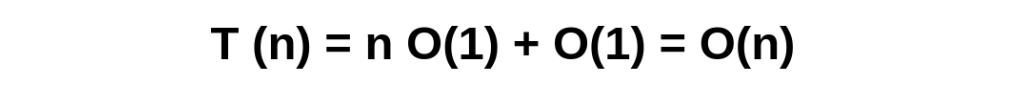Recursion🏃🏽🚶🏽🧑🏽‍🦯

Thinking recursively

Recursion is an important concept in programming and refers to the ability of a function or procedure to call itself within its own definition. That is, instead of solving a problem using a linear approach, the “divide and conquer” technique is used, in which a problem is divided into smaller subproblems that are solved using the same recursive function, until a certain point is reached. base case that can be solved in a trivial way, in a concrete way we can say that it consists of two fundamental parts:

• Base case: It is the simplest case that can be solved without the need to make use of recursion

• Recursive case: This is the case where the recursive function is called to solve a simpler problem

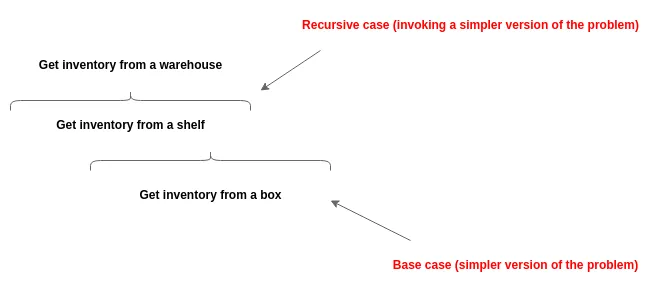
Suppose we have to get the inventory from a warehouse, which has several shelves, and each shelf has several boxes, to solve this problem we can make use of recursion:

Inventory example

Is it necessary to understand recursion to understand recursion?

A bad joke …

To understand recursion, you must understand or at least know the concept of stack but not only as a stack in the field of data structures, but as the stack in memory allocation, the calls to the stack in the stack frame, and finally the recursion and the stack overflow (not the website) which is what happens when the memory limit of the stack is reached, and it occurs a error.

4 interrelated concepts that are fundamental to understanding recursion:

• Stack (Data structures)
• Stack Allocation (Memory allocation)
• Stack Frame (Stack Calls)
• Stack Overflow (Error)

Stack (Data structure)

The stack is a data structure that is characterized by being a type of list in which the access to the elements is done through a single end, which is known as the top.

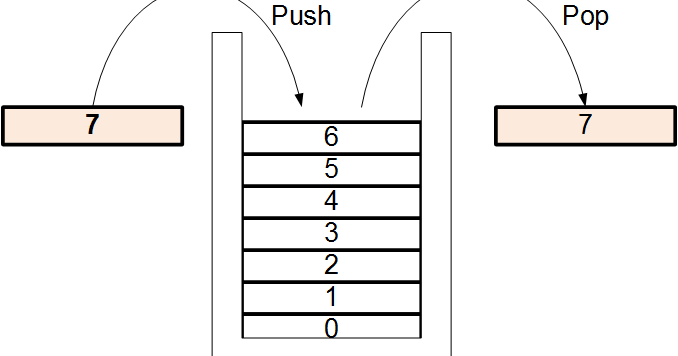Ilustration of how a stack works

This type of structure is used to store data temporarily, so that the last element in is the first out, also known as last in first out (LIFO), when a new element is added to the stack, it is known as push and when an element is removed it is known as pop.

struct Node {
   int value;
   struct Node *next;
};

Node of a stack in C

Stack Allocation (Memory allocation)

Memory allocation refers to the way in wich memory is requested and returned to the computer.

Memory regions

In C there are two ways to allocate memory to variables; Heap Allocation in Heap manages memory at the discretion of the programmer and Stack Allocation in which memory allocation is handled by the compiler.

Stack (Automatic)

• Time of life → Temporary, stores local variables during function calls

• Operation → Faster automatic memory allocation and deallocation than Heap

• Advantages → Easy to use for the programmer and faster than the Heap

• Size → Grows by calling nested functions

• Access → Only from the function that was created

• Freeing → At the end of the show

• Example → Local variables

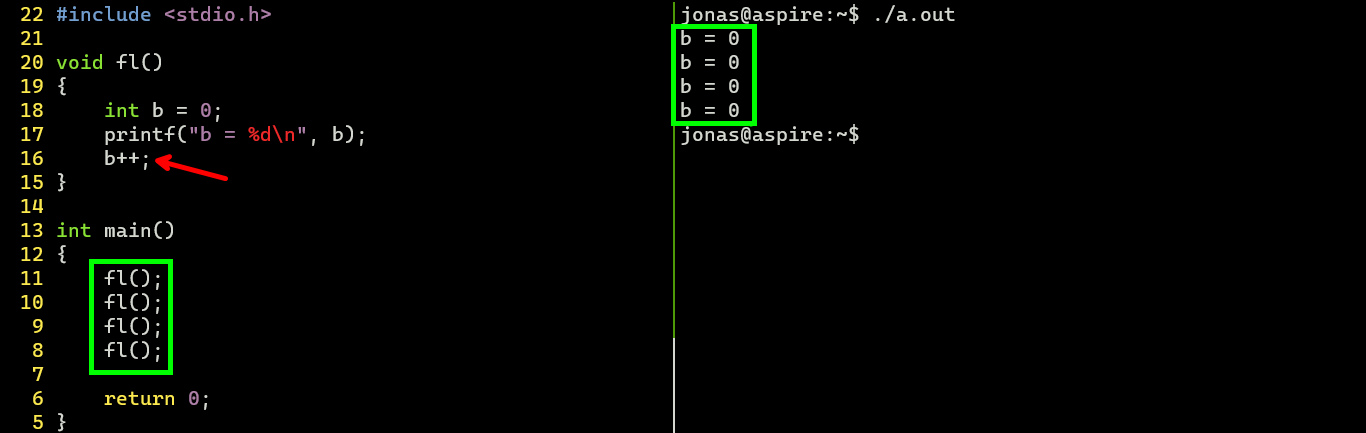This example shows how the operating system automatically creates and destroys the variable b in each of the function calls, preventing a sequence of positive integers from being printed

Stack Frame (Stack Calls)

Call stacks are the calls that are made to the functions in the Stack and these in turn form the Stack frame.

Stack calls

The call stack is a data structure used by most programming languages to keep track of which functions have been called and where they are in the execution of the program. In other words, it is a stack of functions that have been called and are currently being executed.

The stack frame is a record in the call stack that contains information about the current function being executed, such as the return address, function arguments, and local variables.

The Factorial of a Number

To illustrate this, let’s look at an example of recursion in which the factorial of a number is calculated.

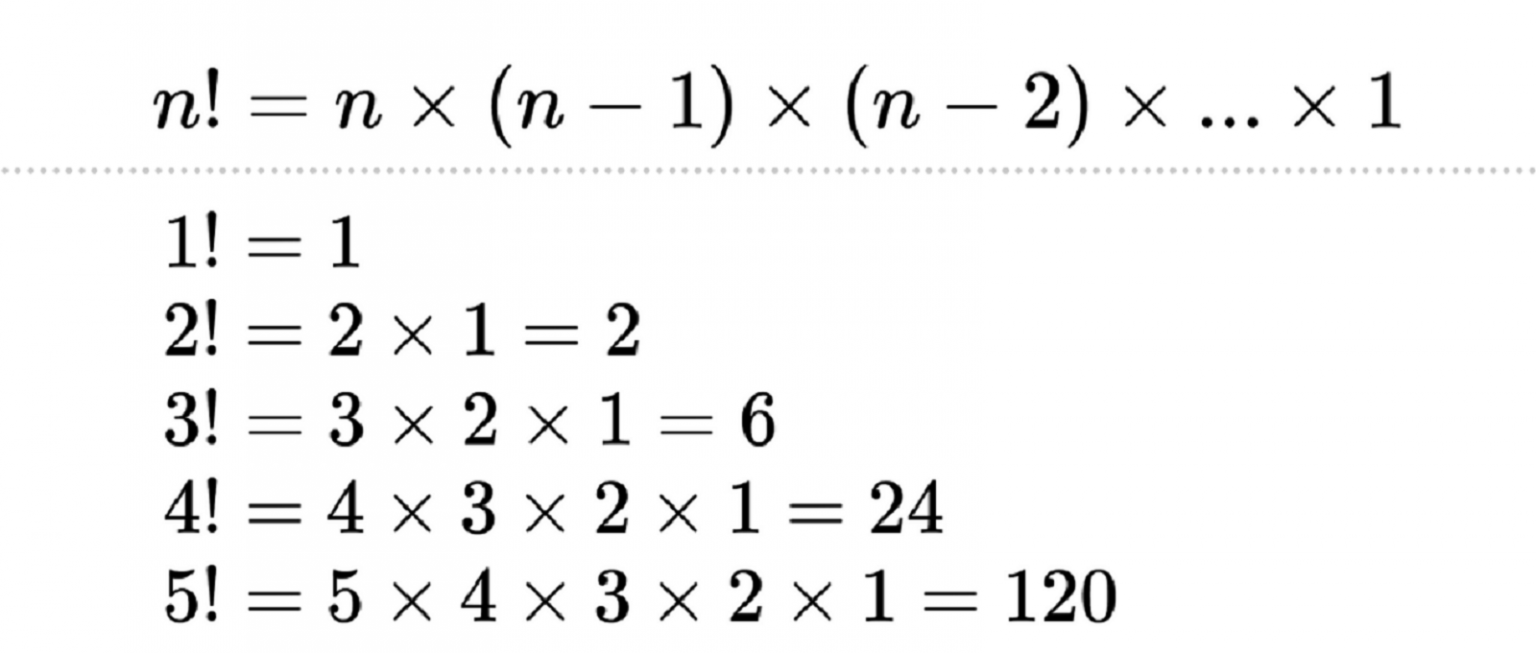Definition and mathematical example of the factorial function

The FACTORIAL of a positive integer is the product of all positive integers up to that.

#include <stdio.h>

int factorial(int n)
{
   if( n < 2 )
    return 1;
   else
    return n * factorial(n-1);
}

int main()
{
   int result = factorial(5);

   printf("Result: %d\n", result);

   //Result: 120

   return 0;
}

Factorial function in C

Step-by-step of the factorial function in C:

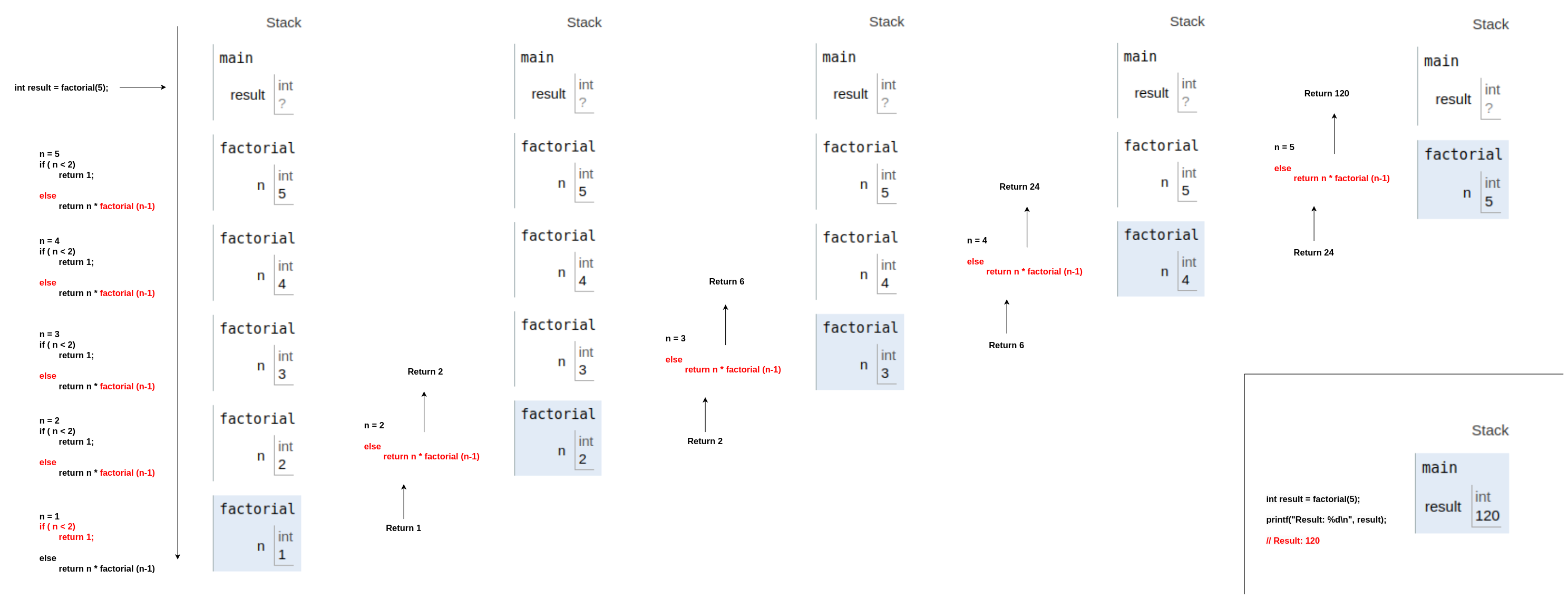From left to right: Step-by-step execution og the factorial function

We can see that the factorial function calls itself until the base case is reached, in which the value 1 is returned and the values of the recursive calls begin to be returned, since the factorial function is a function that returns a value, each time the function is called a new stack frame is created where we are invoking another different function of the same code that lives apart from the other executions where the return value of the function is stored, in this case the value of n * factorial(n-1) and so on until the recursive case is solved.

Asymptotic analysis of factorial function

To analyze the complexity of the factorial function we are going to use the Big O Notation method that allows us to analyze the complexity of an algorithm based on its input, this principle of reaching the base case has its foundation in the principle of mathematical induction.

Operation 1

T(n) it tells us the number of operations that are performed on the factorial n.

Operation 2

In each call we are going to evaluate that T(n) will be given by the constant O(1) operations of the factorial function if n < 2 and return n *, we say that they are constants because they do not depend on the input, that is, no matter the size of the input, the same operations will always be performed, plus T(n-1) which is factorial(n-1) which is the recursive call.

Operation 3

In T(n-1) + O(1), where the terms are reversed for convenience.

Operation 4

The next recursive call would be T(n-2) + O(1) + O(1), because the first entry of T(n-1) and the first entry of O(1) are taken into account.

Operation 5

In the next recursive call it would be T(n-3) + O(1) + O(1) + O(1), because it takes into account the previous inputs of T(n-1) and the first two entries of O(1).

Operation 6

And so on until we reach the base case, where the value 1 is returned plus a number of constant operations O(1) equal to the number of recursive calls.

Operation 7

In the base case we have that T(1) = O(1), so we can say that T(n) = O(n) or of linear complexity, that is, the number of operations that are performed in the factor function is proportional to the size of the input.

Stack overflow (Error)

Stack overflow occurs when the amount of memory allocated to a program’s call stack fills up and there is not enough space to store new stack frames.

Stack overflow website != Stack Overflow

This happens when a large number of recursive function calls are nested, causing the call stack to grow until the available memory is exhausted.

Countdown

A common example of this is countdown where the function is called recursively until it reaches zero:

#include <stdio.h>

static int n = 1000000;

void countDown(int n)
{
     if (0 > n--) return;

     printf("%d\n", n);
    
     countDown(n);
}

int main()
{
     countDown(n);

     return 0;
}

Recursive countdown function in C

Countdown using recursion:

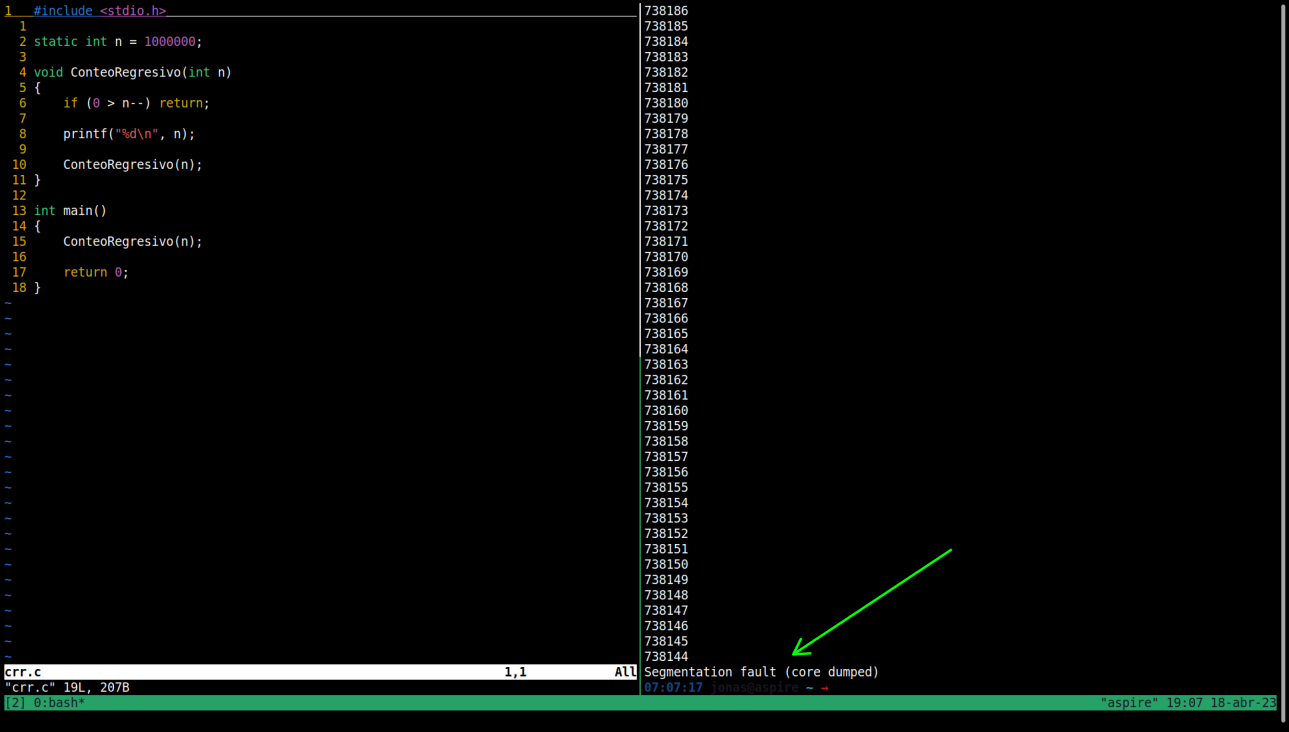Screenshot of the program where memory gets corrupted when filling the stack

Can stack overflow be fixed?

In this case, yes, if we do the implementation iteratively, the stack overflow is not generated:

#include <stdio.h>
#include <stdbool.h>

static int n = 1000000;

void countDown(int n)
{
    while(true)
    {
        switch(n)
        {
            case 0:
                return;
            default:
                printf("%d\n", n);
                n--;
        }
    }
}

int main()
{
     countDown(n);
     printf("Done\n");

     return 0;
}

Iteration countdown function in C

Countdown using iteration:

Executing the program without memory corruption by ensuring that the Stack is not overfilled

Conclusion

With this you can realize that this is one of the most confusing topics in computer science and without a doubt one of the best to understand at the beginning of your career 🧠

References

Cormen, T. H., Leiserson, C. E., Rivest, R. L. & Stein, C. (2009). Introduction to Algorithms (3rd ed.). MIT Press.